About SVM

16 Sep 2018

[ AI  ]

Introduction

I’ve been studying a course unit called Adcanced Signal Processing with deep learning this semester. Actually, it’s not my first time to learn about SVM, I have built up some basic understanding of it in the introduction of AI class last semester. However, to be honest, I still feel lost when I come to Lagrangian formulation. Anyway, I am just trying to some key concepts related to SVM.

In brief, SVM, standing for Support Vector Machine, is a supervised machine learning algorithm that can be implemented for both classification and regression purposes. SVM are more commonly used in classification problems such as text classification tasks, image recognition.

How it works

So, how SVMs achieve that? First we need to know some concepts.

Notation

Say that now we are given l examples, Each example consists of a pair: a vector xi ∈ Rn, i = 1, . . . , l and the associated label yi. With these examples, our machine task is to learn the mapping: xi → yi, so that given any new vector xi, we can predict the label yi. This mapping can also be writted as: xi→ f(x, α), where the functions f(x, α) themselves are labeled by the adjustable parameters α. This also means the machine is assumed to be deterministic: for a given input x, and choice of α, it will always give the same output f(x, α).

Now we take α as a generic set of parameters instead of a single parameter, and we only consider two-class function, that is to say f(x, α) ∈ {−1, 1} ∀x, α. We use {f(α)} to represent a set of functions, as a choice of α specifies a particular function.

Hyperplane

In geometry, a hyperplane of an n-dimensional space V is a subspace of dimension n − 1, or equivalently, of codimension 1 in V.

For example, for a classification task with only two features (in 2D space), then a hyperplane would be a line that linearly separates and classifies a set of data.

Shattered Set

shattered sets is an important concept in VC-Theory.

Suppose A is a set and C is a class of sets. The class C shatters the set A if for each subset a of A, there is some element c of C such that: a = c∩A

The VC dimension

The VC dimension is a property of a set of functions {f(α)},

Now if a given set of l points can be labeled in all possible 2l ways, and for each labeling, a member of the set {f(α)} can be found which correctly assigns those labels, we say that that set of points is shattered by that set of functions. The VC dimension for the set of functions {f(α)} is defined as the maximum number of training points that can be shattered by {f(α)}.

For example, suppose we have a set of data points with Oriented Hyperplanes in R^2, and the set {f(α)} consists of oriented straight lines, so that for a given line, all points on one side are assigned the class 1, and all points on the other side, the class −1.The orientation is shown in Figure below by an arrow, the side of the line points are to be assigned the label 1.

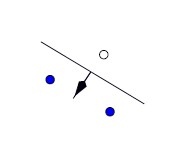
So, what’s maximum number of points can be classified by this set {f(α)}? As shown below, it is possible to find three points that can be shattered by this set of functions, it is not possible to find four. 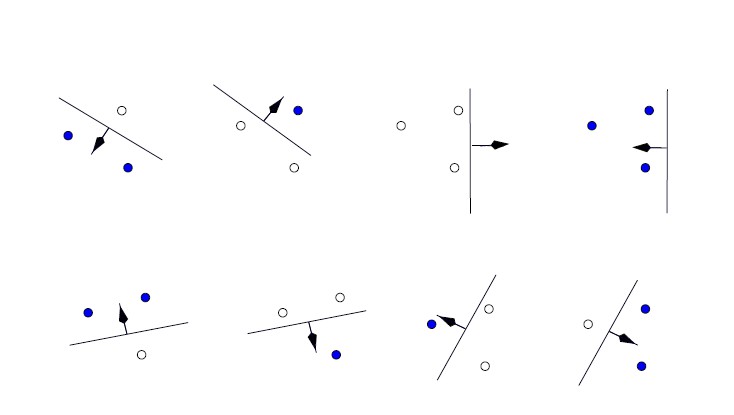Thus the VC dimension of the set of oriented lines in R2 is three.

Reference

Malon, C., Uchida, S. and Suzuki, M. (2008). Mathematical symbol recognition with support vector machines. Pattern Recognition Letters, 29(9), pp.1326-1332.